回路理論とSPICEシミュレーション


SPICEで学ぶ電気回路の基礎　講座

How to use >　目次　　　　　　　【他のページへは目次のリンクよりジャンプして下さい】

６．　磁気結合回路

６．１　相互誘導

単独のインダクタについての電圧電流の関係式（電磁誘導）	コイルに流れる電流により発生する鎖交磁束（鎖交磁束数）は、電流に比例する。比例定数をインダクタンスと呼ぶ。 N回巻きのインダクタンスL[H]のコイルに流れる電流 i [A]により発生した鎖交磁束（巻数N×磁束φ）をΦ[Wb]とすると、　　　Φ=Nφ=Li と表される。（この式はアンペール（-マクスウェル）の法則に由来している。） N回巻のコイル両端の電圧、つまり誘導起電力v は、ファラデーの電磁誘導の法則により、磁束鎖交Φの時間的変化率に等しい。　　　v=dΦ/dt=N ･dφ/dt=Ldi/dt　------ (6.1) と表される。（第3章に示したインダクタについての電圧･電流の関係式。）この式は上記のようにファラデーの法則に由来している。
相互誘導	ここで、コイルが二つあり、片方のコイル1にのみ電流を流すとする。他方のコイル2にコイル1による磁束φ21が鎖交するとすると、巻き数N2のコイル2に発生する起電力v2は(6.1)式より　　　v2=N2 ･dφ21/dt　----- (6.2) で表される。コイル自分自身による磁束ではなく、他のコイルによる磁束でも、誘導起電力が発生することを示している。この現象を相互誘導作用と呼ぶ。また、一般的に、コイルの巻数をN、コイルの形状で決まる任意の比例定数をαとすると発生する磁束φは　　　φ=αNi　------　(6.3) と表すこともできる。また、ここでコイル1の巻き数をN1とすると、(6.3)式より　　　φ21=α1 ･N1 ･i1 これを(6.2)式に代入して　　　v2=N2 ･dφ21/dt=α1 ･N1 ･N2 ･di1/dt この式の比例定数部分をM21とすると、　　　v2=M21 ･di1/dt　-------- (6.4) 次に逆に、コイル2にのみ電流を流すと、コイル1にはコイル2による磁束φ12が鎖交する。コイル1に発生する起電力v1は　　　v1=N1 ･dφ12/dt=α2 ･N1 ･N2 ･di1/dt 上記と同様にして以下のように表される。　　　v1=M12 ･di2/dt --------- (6.5)
相互インダクタンス	上で示したM12やM21を相互インダクタンスと呼ぶ。対照的にL1やL2を自己インダクタンスと呼ぶ。前項の議論より、2つのコイル1,2が磁気結合していて、1次側電圧電流がそれぞれv1，i1、2字側電圧電流がv2，i2である回路には以下の式が成り立つ。　　　v1=L1 ･di1/dt+M12 ･di2/dt 　　　v2=L2 ･di2/dt+M21 ･di1/dt ここで、M12とM21は2つのコイルの形状、位置関係だけによって決まるので、固定された回路ではM12=M21といえる（正確には数式で求まる）ので、これを相互インダクタンスMとおく。したがって　　　v1=L1 ･di1/dt±M ･di2/dt ------- (6.6) 　　　v2=L2 ･di2/dt±M ･di1/dt ------- (6.7) 入力を正弦波として複素記号法で表せば（ここの太字記号は複素数を示す）、　　　V1=jωL1I1±jωMI2 ---------- (6.8) 　　　V2=jωL2I2±jωMI1 ---------- (6.9) 相互インダクタンスMの符号がプラスとマイナスの場合があるのは、2つのコイルの巻き線の向きと流れる電流によって、生じる磁束、それにより発生する電圧の向きが一致するか逆かによる。磁束、発生電圧の向きが一致していればプラスになり、逆向きであればマイナスである。これは、回路図ではドットを使って表すことができる。一般的には、1次2次コイルの巻き線の片方にドットをつけ、1次コイルのドットがある側から電流が流れ込んだときに、2次コイルのドットがある側に正の電圧が発生すると決められている。
結合係数	エネルギー（仕事）w(t)は、パワー（電力、仕事率）p(t)を時間で積分したものである。インダクタの自己インダクタンスにより蓄積されるエネルギーは、p=vi，v=Ldi/dtよりｗ(t)=∫p(t)dt[0→t]=∫Ldi/dt ･idt=L∫idi[i0→i]=1/2 ･L(i^2-i0^2)=Li^2/2 相互インダクタンスにより蓄積されるエネルギーは、p=v1 ･i1，v1=Mdi2/dtより、1次コイルの磁気エネルギーはｗ1(t)=∫p(t)dt[0→t]=∫Mdi2/dt ･i1dt=Mi1i2 したがって、2つの磁気結合したコイルに蓄積される全エネルギーは　　　w=L1i1^2/2+L2i2^2/2+Mi1i2 -------- (6.10) (6.10)式を次のように代数変形する。　　　w=L1/2 ･(i1+Mi2/L1)^2+1/2 ･(L2-M^2/L1) ･i2^2 ここでwは正でなければならない。特にi1=-Mi2/L1のときでも、wは正でなければならない。したがって、L2-M^2/L1≧0である。よって L1L2≧M^2でなければならない。つまり、\|M\|≦√(L1L2)。これを結合係数 k という値を使って　　　M=k√(L1L2) ------------------- (6.11) と表す。kは、0≦k≦1（またはMが負のときも含めて-1≦k≦1とする場合もある） k=0とは：　2つのコイルがまったく磁気結合していない場合。 k=1とは：　2つのコイルが理想的に磁気結合している。片方のコイルで生じた磁束がすべてもう一方のコイルを鎖交する。したがって、結合係数 k が1に近いか0に近いかで、2つのコイルの磁気的結合の度合いが簡単にわかる。

６．２　理想変成器とT型等価回路

変成器	電磁誘導を利用して、交流電圧を簡単に昇圧・降圧（変圧）したり、入出力インピーダンスの変換や整合などに使われる。鉄心（コア）と呼ばれる磁気の通り道および巻き線の芯になる部分の周りに、通常2本以上の導線を巻き、端子をつけた構造とする。トランス（Transformer）または、電圧の変換用と明確ならば、変圧器とも呼ばれる。
磁気結合回路	上図に示すAC電圧源Eとトランスと任意のインピーダンスZ1,Z2からなる回路を考える。これは、これ以上省略ができない磁気結合回路の基本回路ということができる。式(6.8)(6.9)から（太字記号は複素数を示す）、　　　V1=jωL1I1+jωMI2=E-Z1I1 ---------------------- (6.12) 　　　V2=jωL2I2+jωMI1=-Z2I2 ----------------------- (6.13) 行列式にまとめて、電流について解くと、　　　I1=(jωL2+Z2)E/{(jωL1+Z1)(jωL2+Z2)+ω^2M^2} ------ (6.14) 　　　I2=-jωME/{(jωL1+Z1)(jωL2+Z2)+ω^2M^2} ---------- (6.15) (6.14)を(6.12)の第3式に代入して　　　V1=E-Z1I1 　　　　 ={jωL1(jωL2+Z2)+ω^2M^2}E/{(jωL1+Z1)(jωL2+Z2)+ω^2M^2} ---- (6.16) (6.15)を(6.13)の第3式に代入して　　　V2=-Z2I2 　　　　=jωMZ2E/{(jωL1+Z1)(jωL2+Z2)+ω^2M^2} -------------------- (6.17) 電源から負荷側をみた回路の入力インピーダンスをZinとすると、(6.14)式より　　　Zin=E/I1=Z1+jωL1+ω^2M^2/(jωL2+Z2) ------------ (6.18)
理想変成器	コイルとコイルの磁気結合が完全な場合、つまり結合係数 k=1（M=√(L1L2))である変成器を密結合変成器と呼ぶ。 (6.16)(6.17)式とM=√(L1L2)を使って、2次側コイル電圧V2と1次側コイル電圧V1の比を計算する。　　　V2/V1=jωMZ2/(-ω^2L1L2+jωL1Z2+ω^2M^2) 　　　　　　　　=M/L1=√(L2/L1) -------------------------- (6.19) (6.14)(6.15)式を使って、2次側コイル電流I2と1次側コイル電流I1の比を計算する。　　　I2/I1=-jωM/(jωL2+Z2) ここで、jωL2>>Z2とすると　　　I2/I1=-M/L2=-√(L1/L2) ------------------------- (6.20) ここで密結合変成器なので、鎖交磁束をΦとすると、以下の関係が成り立つ。　　　N1Φ=L1i1，　N1Φ=Mi2 　　　N2Φ=L2i2，　N2Φ=Mi1 よって、M/L1=N2/N1とM/L2=N1/N2が得られる。これらを(6.19)と(6.20)にそれぞれ代入して、　　　V2/V1=√(L2/L1)=N2/N1 ------------------------- (6.21) 　　　I2/I1=-√(L1/L2)=-N1/N2 ------------------------- (6.22) (6.21)(6.21)式を満たすような変成器を理想変成器と呼ぶ。理想変成器で、エネルギーがどう送られるかを考えると、(6.21)(6.22)式を使って　　　(I2V2)/(I1V1)=(N1N2)/(N1N2)=-1　　（V2という表現はV2の共役複素数を表す。4.3節参照）したがって、理想変成器では入力された電力がすべて負荷に送られる。理想変成器を考えることで、理想的な場合という条件がつくが、変成器の基本的な特性が理解できる。 (6.18)において、密結合なのでM=√(L1L2)、およびjωL2>>Z2とすると　　　Zin*=Z1+jωL1+ω^2M^2/(jωL2+Z2) =Z1+(-ω^2L1L2+ω^2M^2+jωL1Z2）/(jωL2+Z2) 　　　　　 =Z1+L1Z2/L2=Z1+Z2(N1/N2)^2 ----------------- (6.23) 上式は、入力1次側からみた負荷インピーダンスZ2が、(N1/N2)^2倍になっていることを示している。変成器がインピーダンス変換の素子として利用できることがわかる。
T型等価回路	厳密に考えると、磁気結合した2つのコイルには、共通の端子はない。しかし、ドットで示されるコイルの極性にさえ注意すれば、2つのコイルの基準となる電位を共通であるとしても問題はない。相互インダクタンスMの磁気結合回路の電圧電流の関係式(6.6)(6.7)を、以下のように変形する。　　　v1=L1di1/dt+Mdi2/dt=(L1-M)di1/dt+Md(i1+i2)/dt 　　　v2=L2di2/dt+Mdi1/dt=(L2-M)di2/dt+Md(i1+i2)/dt この2式を回路図で表すと下図(b)のようになる。これは変形前の図(a)の等価回路である。これをトランスのT型等価回路と呼び、トランスを含んだ回路解析を容易にしてくれる。図(b)にはドットは不要である。図(a)の回路で2つのコイルの極性が逆の場合は、M→-Mとおけばよい。
変成器の入出力電圧電流の近似式	式(6.14)～(6.17)で入出力電圧電流が求められたが、近似条件を用いてよりわかりやすい式に変形してみる。 (6.16)より　　　V1={jωL1(jωL2+Z2)+ω^2M^2}E/{(jωL1+Z1)(jωL2+Z2)+ω^2M^2} ここで、jωL1>>Z1とすると、　　　V1≒E ----------------------- (6.24) (6.17)より　　　V2=jωMZ2E/{(jωL1+Z1)(jωL2+Z2)+ω^2M^2} ここで、jωL1>>Z1　および　k≒1とすると、　　　V2≒√(L2/L1)・E ----------------------- (6.25) (6.14)より　　　I1=(jωL2+Z2)E/{(jωL1+Z1)(jωL2+Z2)+ω^2M^2} ここで、jωL1>>Z1　および　k≒1とすると、　　　I1≒(ωL2-jZ2)E/(ωL1Z2) 　　　　　=\|E\|・√(ω^2・L2^2+Z2^2)/(ωL1Z2)∠tan-1(-Z2/ωL2) ----------------------- (6.26) 　　(1)　Z2>>jωL2とすると、　　　tan-1(-Z2/ωL2)=-90°、\|I1\|=\|E\|/(ωL1) 　　(2)　Z2<<jωL2とすると、　　　tan-1(-Z2/ωL2)=0°、\|I1\|=\|E\|L2/(L1Z2) (6.15)より　　　I2=-jωME/{(jωL1+Z1)(jωL2+Z2)+ω^2M^2} ここで、jωL1>>Z1　および　k≒1とすると、　　　I2≒-ME/(L1Z2)=-√(L2/L1)・E/Z2 ----------------------- (6.27)

６．３　理想変成器を使った等価回路

理想変成器を使って、トランスの等価回路を考える。トランスの基本機能を、理想変成器に置き換えることにより、トランス特性を各成分ごとに分けることが容易になる。実測した各成分をこの等価回路に当てはめることにより、実物特性により近い等価回路が得られる。等価回路例1～3は、理想変成器と相互インダクタンスのみを表した等価回路。より詳細な等価回路を考える場合には、これに、鉄損（ヒステリシス損＋渦電流損）、銅損（巻き線の抵抗分）、巻線間容量などを追加する（等価回路例４：ただし鉄損を線形として扱う）。また、ここではとり上げないが、SPICEなどのシミュレーションでは、鉄損を非線形要素として扱えるモデルも使われている。
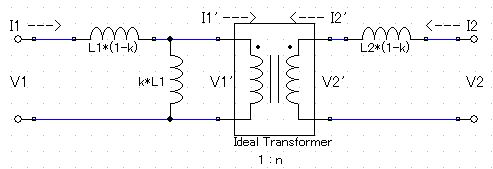
等価回路例１（相互インダクタンスのみ）	この回路が式(6.8)と(6.9)を満たせば、正しい等価回路と言える。　　　V1=jωL1(1-k)I1+V1' 　　　　 =jωL1(1-k)I1+jωkL1(I1-I1') 　　　　　=jωL1(1-k)I1+jωkL1(I1+I2√(L2/L1)) 　　　　　=jωL1I1+jωMI2 　　　V2=jωL2(1-k)I2+V2' 　　　　 =jωL2(1-k)I2+√(L2/L1)V1' 　　　　　=jωL2(1-k)I2+jωkL1(I1+I2√(L2/L1))√(L2/L1) 　　　　　=jωL2I2+jωMI1 ただし、V2'/V1'=n=√(L2/L1)、I2/I1'=-√(L1/L2)、M=k√(L1L2)
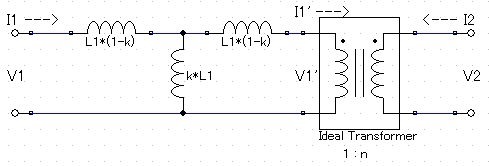
等価回路例２（相互インダクタンスのみ）	この回路は、上記例１の2次側のインダクタンスを1/n^2して、1次側に換算したものである。換算法は、2次側に入っているインピーダンスは直並列に関係なく、1/n^2倍し（巻き数比1：n）、1次側にそのままの順番で平行移動する。R，Lは、それぞれ、R/n^2，L/n^2、Cは、Cn^2となることに注意。わざわざ片側に換算する理由は、実際のトランス特性を計測する場合に、1次側に換算していれば1次側からの測定だけで済ますことができるため（ネットワーク･アナライザ等を用い、2次側を開放、短絡して測定）。この回路が式(6.8)と(6.9)を満たせば、正しい等価回路と言える。　　　V1=jωL1(1-k)I1+jωkL1(I1-I1') 　　　　　=jωL1(1-k)I1+jωkL1(I1+I2√(L2/L1)) 　　　　　=jωL1I1+jωMI2 また、V1=jωL1(1-k)I1+jωL1(1-k)I1'+V1'であるから　　　V1'=V1-jωL1(1-k)I1-jωL1(1-k)I1' 　　　　　=jωL1I1+jωMI2-jωL1(1-k)I1-jωL1(1-k)(-I2√(L2/L1)) 　　　　　=jωkL1I1+jω√(L1L2)I2 　　　V2=√(L2/L1)V1' 　　　　 =jωk√(L1L2)I1+jωL2I2 　　　　=jωL2I2+jωMI1 ただし、V2/V1'=n=√(L2/L1)、I2/I1'=-√(L1/L2)、M=k√(L1L2)
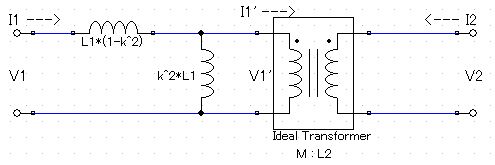
等価回路例３（相互インダクタンスのみ）	上記の回路と同じ理由で、2次側特性（この場合2次側漏れインダクタンス）を1次側に換算している。この回路が式(6.8)と(6.9)を満たせば、正しい等価回路と言える。　　　V1=jωL1(1-k^2)I1+V1' 　　　　 =jωL1(1-k^2)I1+jωk^2L1(I1-I1') 　　　　　=jωL1(1-k^2)I1+jωk^2L1(I1+L2I2/M) 　　　　　=jωL1I1+jωMI2 　　　V2=L2V1'/M 　　　　 =jωk^2L1(I1+L2I2/M)L2/M 　　　　 =(jωk^2L1L2I1+jωk^2L1L2^2I2/M)/M 　　　　　=jωL2I2+jωMI1 ただし、V2/V1'=L2/M、I2/I1'=-M/L2、M=k√(L1L2)
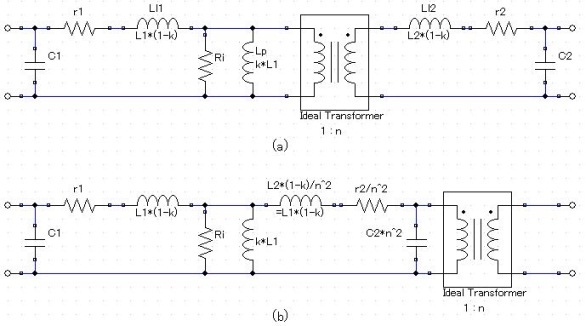
等価回路例４（相互インダクタンス＋その他）	図(a)の素子の意味 Lp：励磁インダクタンス、Ll1：1次巻き線漏れインダクタンス、Ll2：2次巻き線漏れインダクタンス、巻き数比N1：N2=1：n、 Ri：鉄損、r1：1次巻き線抵抗、r2：2次巻き線抵抗、C1：1次巻き線浮遊容量、C2：2次巻き線浮遊容量、図(b)は、図(a)の2次側の素子を1次側に換算した場合。
SPICEによる確認：トランスのSPICE基本形とその他の等価回路
SPICE回路図ファイル	K_inductive_coupling_T.sch (TopSpice 8 回路図ファイル)
クリックで拡大
回路図の作成	周波数50Hz、AC100Vを降圧する電源トランスをイメージした回路定数です。SPICEでトランスを構成するときの基本形と、これまで出てきた等価回路合計5種類を一つの回路図に入力しました。各種定数は、変更する場合に5回路分直すのが大変なので、.PARAMコマンドにより変数にしています。一箇所の定数を変更すれば、5回路分が同時に変わります。 SPICE基本形のトランスは、インダクタL素子二つと、インダクタ結合K素子で構成します。K素子において、どのインダクタ（2個以上可能）を結合させるかと、結合係数ｋを設定します（バークレーSPICE2、SPICE3では二つのインダクタしか結合できません）。これらのLとK素子は、回路図上でどこに配置しても機能上はかわりありませんが、図のようにそれらしく近づけて配置します。サブサーキットX1～X3は、理想変成器で、アナログ・ビヘイビア･モデルです。従属電源で自分で作ることもできますが、ほとんどの商用SPICEにはライブラリに入っているはずです。
解析の設定と実行（過渡解析）	定常時の波形を見るために、時間20ms～80msとしています（0sの波形を気にしなければ、0～60msでもかまいません）。正弦波なので、例によって最大時間ステップを60ms/1000=60usと設定します。信号源の初期位相90°とインダクタの初期電流IC=0Aは、第3章と同じ理由によります。
解析結果の検討	5回路の電圧電流がそれぞれ一致しているので、T型等価回路、理想変成器を使った等価回路の定数設定があっていることがわかります。電圧電流それぞれの振幅と位相関係も、式(6.24)～(6.27)と合致した結果となっています。
SPICEによる確認：全波整流回路（センタータップ型）
SPICE回路図ファイル	Full-Wave_Rectifier_test.sch (TopSpice 8 回路図ファイル)
クリックで拡大
回路図の作成	巻き線が3本の場合の例として、センタータップ型全波整流回路をとり上げます。TopSpiceシミュレータのデモ版にも、同様の回路が添付されていますが、そちらはサブサーキットを使っています。その内部接続をL素子、K素子で書き換えました。また、素子定数も一度で変更できるように変数化しています。ダイオードは、本講座の範疇を外れるものものですが、基本の整流機能を見るだけなので使用しました。ダイオードの特性を決めるモデル･パラメータは、回路図内の.MODELコマンドで示されるように、指定なしであり、すべてデフォルト値が使われています。なお全波整流回路としては、トランスにセンタータップが不要でネックとなるトランスの小型化に有利な、ブリッジ型全波整流回路の方がよく使われます。ダイオードが4つ必要ですが、4つが1パッケージに収められたブリッジ･ダイオードが多く市販されています。
解析の設定と実行（過渡解析）	定常時の波形を見るために、時間20ms～60msとしています。正弦波なので、例によって最大時間ステップを40ms/1000=40usと設定します。信号源の初期位相90°とインダクタの初期電流IC=0Aは、第3章と同じ理由によります。
解析結果の検討	全波整流が正しく行われています。電圧電流それぞれの振幅と位相関係が、式(6.24)～(6.27)と合致した結果となっています。出力OUTに、平滑コンデンサを入力すると、DC出力が得られます。キャパシタの容量を変えて、リップルの変化を見たり、またキャパシタをより正確な等価回路で表したりと、実験が可能です。

Home | What's Simulation | How to use | Links | Books | Services | About us | Contact us | Blog

Copyright(C) 2011 SimCircuit Technologies Co., Ltd.