| 次の図に示す基本的な5つの回路について、ラプラス変換を使用して回路電流を求めたいとする。要点は、表10-1と10-2が使えるような代数式の変形ができるかどうかになる。色々な回路例を試して、部分分数展開の手法に慣れる必要がある。 |
直流電源とRC直列回路
|
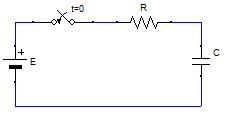回路方程式は、
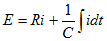表10-1と10-2の積分の変換に基づき、両辺をラプラス変換する。ここで、キャパシタの初期電荷をq0=C・v0とする。
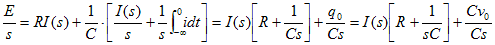電流について解き、表10-1を使ってラプラス逆変換できるように、変形を行う。
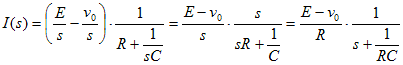表10-1と、表10-2の線形性を使い、ラプラス逆変換を行う。
 |
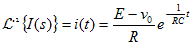---- (10.1) |
|
| 直流電源とRL直列回路 |
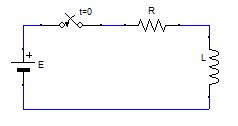
回路方程式は、
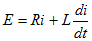
表10-1と10-2の1階微分の変換に基づき、両辺をラプラス変換する。ここで、インダクタの初期電流をi0とする。
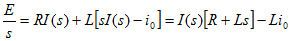
電流について解き、表10-1と10-2を使ってラプラス逆変換できるように、変形を行う。
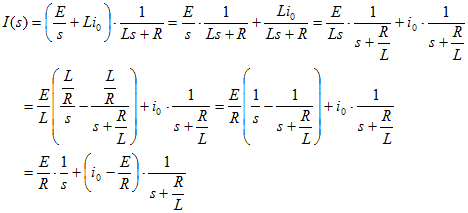
なお、上記の計算途中で、以下の部分分数展開を使用している。
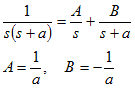
従って、I(s)をラプラス逆変換すると、
 |
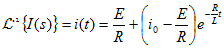---- (10.2) |
|
| 交流電源とRC直列回路 |
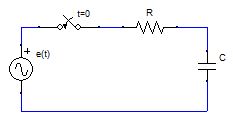
回路方程式は、
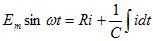
表10-1と10-2の積分の変換に基づき、両辺をラプラス変換する。ここで、キャパシタの初期電荷をq0=C・v0とする。
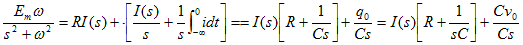
電流について解き、ラプラス逆変換できるように、部分分数展開を行う。
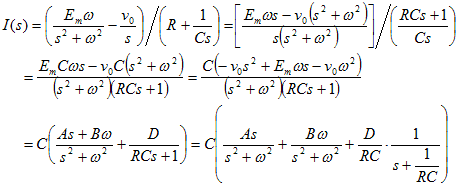
ただし、部分分数展開する前後の分子の各項を比較して
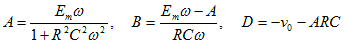
I(s)をラプラス逆変換すると、
 |
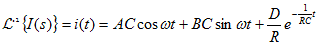---- (10.3) |
|
| 交流電源とRL直列回路 |
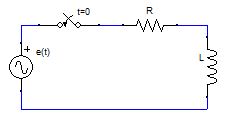
回路方程式は、
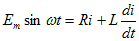
表10-1と10-2の1階微分の変換に基づき、両辺をラプラス変換する。ここで、インダクタの初期電流をi0とする。
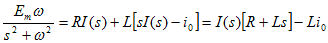
電流について解き、表10-1を使ってラプラス逆変換できるように、変形を行う。
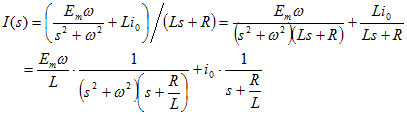
ここで、部分分数展開を書き出してみると、
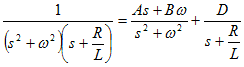
分子を計算し、両辺の分子を等しいとすると、
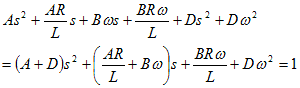
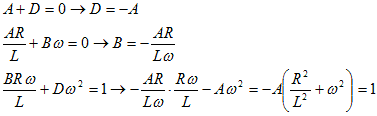
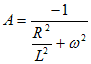
上記の結果を使って、
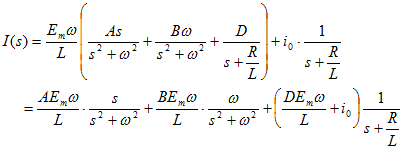
I(s)をラプラス逆変換すると、
 |
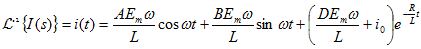---- (10.4) |
|
| 直流電源とRLC直列回路 |
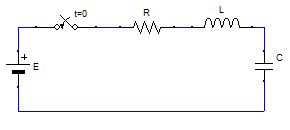
回路方程式は、
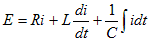
表10-1と10-2に基づき、両辺をラプラス変換する。ここで、インダクタの初期電流をi0、キャパシタの初期電荷をq0=C・v0とする。
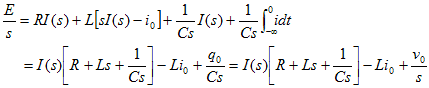
電流について解き、表10-1と10-2を使ってラプラス逆変換できるように、変形を行う。
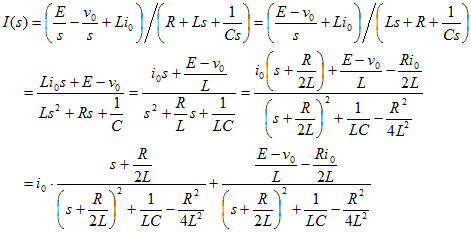
なお、上記で行った部分分数展開は、下記のルールを使用している。
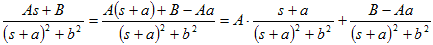
ラプラス変換の表に従い変換するに当たり、I(s)の最終式の分母の後半部がとる値により、以下の3つの場合分けがされる。
 |
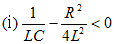
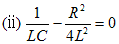
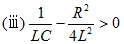
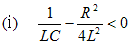
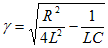とおくと、 |
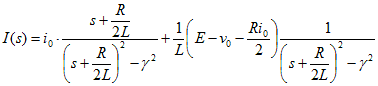
表10-1の双曲線関数の変換と表10-2の周波数移動の法則により、ラプラス逆変換すると、
 |
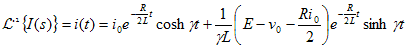---- (10.5) |
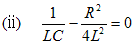
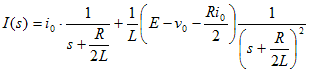
表10-1によりラプラス逆変換を行うと、
 |
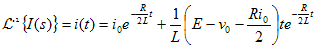---- (10.6) |
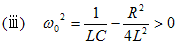
表10-1によりラプラス逆変換を行うと、
 |
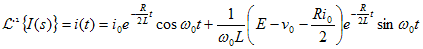---- (10.7) |
|
以下で本章の内容をSPICEで確認していますが、ラプラス変換で求めた解をビヘイビア電源で発生させ、SPICE過渡解析アルゴリズムの結果と比較するというものです。これは、途中の紙と鉛筆による計算の方法が違うだけで、SPICEの使い方としては、前章と同じです。
市販の多くのSPICEには、伝達関数を記述できるラプラス電源機能（過渡解析、AC解析で使用可能）がついています。これを利用した各種回路図ファイルは、次章で紹介予定です。 |
| SPICEによる確認： 直流電源とRC直列回路 |
| SPICE回路図ファイル |
Initial_Condition_RC.sch (TopSpice 8 回路図ファイル） |
.jpg) .jpg) クリックで拡大 |
| 回路図の作成 |
RC直列回路にスイッチONで直流電源を印加する場合に流れる電流を、上記でラプラス変換により求めました。この求めた数式(10.1)をアナログ・ビヘイビア電源に記述して電流を発生させた場合と、SPICEで回路を作成し、回路電流をで普通に求める場合とを比較します。
なお、スイッチは動作を分かりやすくするためだけに入れた、ただのダミーです。削除し短絡しても構いません。
|
解析の設定と実行
（過渡解析）
|
キャパシタの初期電荷q0=0の場合と、q0=C・v0=C・2Vの場合を、パラメトリック解析で行わせます。グラフ上段は、v0=0のときのSPICE解析と数式による計算結果です。グラフ下段は、v0=2VのときのSPICE解析と数式による計算結果です。
TopSpiceの波形表示プログラムTopViewの機能により、パラメトリック解析の1回目の結果をグラフ上段に、2回目の結果をグラフ下段に振り分けて表示させています。
|
| 解析結果の検討 |
SPICEの過渡解析アルゴリズムによる波形I(R1)と、ラプラス変換で求めた解の式による波形I(R2)は、完全に一致し、求めた解の数式が合っていることが確認できます。簡単な式なので、初期電荷（電圧）により回路の初期電流がどう決まるかが読み取れます。 |
| SPICEによる確認： 交流電源とRL直列回路 |
| SPICE回路図ファイル |
Initial_Condition_RL_sin.sch (TopSpice 8 回路図ファイル） |
.jpg) .jpg) クリックで拡大 |
| 回路図の作成 |
RL直列回路にスイッチONで交流電源を印加した場合です。数式は、上記の(10.4)式を使っています。かなり複雑な数式ですが、SPICEのビヘイビア電源では、上記で求めたとおりに任意の変数を.PARAMコマンドで指定できるので、そのまま根気強く入力するだけで実現できます。
|
解析の設定と実行
（過渡解析）
|
インダクタの初期電流i0=0Aの場合と、i0=5mAの場合を、パラメトリック解析で行わせます。グラフ上段は、i0=0のときのSPICE解析と数式による計算結果です。グラフ下段は、i0=5mAのときのSPICE解析と数式による計算結果です。
|
| 解析結果の検討 |
SPICEの過渡解析アルゴリズムによる波形I(R1)と、ラプラス変換で求めた解の式による波形I(R2)は、完全に一致し、求めた解の数式が合っていることが確認できます。(10.4)式と波形を見比べると、過渡現象は、指数関数項が決定していることが分かります。 |
| SPICEによる確認： 直流電源とRLC直列回路 |
| SPICE回路図ファイル |
Initial_Condition_RLC.sch(TopSpice 8 回路図ファイル） |
.jpg) .jpg) クリックで拡大 |
| 回路図の作成 |
RLC直列回路にスイッチONで直流電源を印加した場合です。数式は、上記の(10.5)〜(10.7)式を使っています。この3つの式は、場合分けなので本来は同一ですが、これを一つのビヘイビア電源で表すことは困難なので、3回路として併記しています（上の拡大図では2回路のみしか表示していません。回路図ファイルには入っています）。RLC回路図の方は、Rを可変にして一つで間に合わせます。 |
解析の設定と実行
（過渡解析）
|
初期電圧v0、初期電流i0は、それぞれの変数値を設定できますが、取り敢えずどちらも0としておきます。グラフの表示は、上段より過制動：I(R1)@R=2k,
I(R(2)、臨界制動：I(R1)@R=632.5, I(R(3)、減衰振動：I(R1)@R=100, I(R(4)とし、各場合ごとに、SPICE解析と数式入力の結果を比較表示します。 |
| 解析結果の検討 |
SPICEの過渡解析アルゴリズムによる波形I(R1)と、ラプラス変換で求めた解の式による波形I(R2)〜I(R4)は、完全に一致し、求めた解の数式が合っていることが確認できました。
前章の内容をこの回路に合わせて再掲します。
| 過制動： |
R=2k>2√(L/C) |
一度増加した値が振動をしないで減少する（回路電流の場合）。 |
| 臨界制動： |
R=632.455=2√(L/C) |
過制動と減衰振動の境界。一度増加した値が指数関数に従い減少する。（回路電流の場合） |
| 減衰振動： |
R=100<2√(L/C) |
正弦波が指数関数的に減衰する（回路電流の場合）。 |
|
