| たたみ込み積分とは |
たたみ込み積分(合成積)は、前章で簡単に紹介したが、回路理論の他、システム論や制御理論で重要な演算である。なお、たたみ込み積分の概念自体は、ラプラス変換とは独立しているものである。
過去のある瞬間にf1という事象が起こり、それが時間的変化を伴う増幅や減衰という一定の要因f2により変化させられて、結果が現在現れると仮定できる何らかの仕組み(システム)があると考える。(注1)
過去の事象が複数回発生したときには、結果は複数回の事象の加算と考えられる。これは時間で積分することに等しい。現在時刻をtとして、その結果を考える。時刻τに発生した事象f1(τ)に対して、発生時から現在までの時間経過がt-τとなるので、f2(t-τ)で表される増幅や減衰を伴う変化が加えられるので、結果として現れる影響はf1(τ)f2(t-τ)で表される。複数の事象を考慮すると、全体の結果は、f1(t),
f2(t)が因果律を満たすならば、任意の事象が起こった時刻τについての積分をτ=0からτ=tまで行えば良いので、下記式で表される。
なお、f1(t-τ)f2(τ)としても結果は同じになる
(理由およびたたみ込み積分のより分かりやすい解説は下記参考サイトを参照)。
|
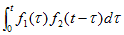 |
|
|
これを一般的に表すと、 |
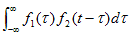 |
参考:「初心者用畳み込み(たたみこみ)解説」 東北工業大学 情報通信工学科 中川研究室
この解説で考えているシステムは「人生」。
(注1):たたみ込み積分が成り立つシステムの厳密な定義は、線形時不変なシステム。
・線形性とは、入出力が比例関係にあること。詳しく述べると、色々な入力があったときに出力は単独の入力に対するそれぞれの出力の足し算で表せること、つまり重ね合わせができることである。
・時不変性とは、時刻によりシステムの特性が変動せず、入力の時刻が変わっても出力がその分シフトされるだけで現れることである。
|
| たたみ込み積分のシステム解析(回路解析)への応用 |
あるシステム(ここでは回路)に、単位インパルスδ(t)を加えたときの出力をh(t)とする。h(t)は、インパルス応答と呼ばれる。単位インパルスを加える時刻をτとすると、現在時刻
t における出力は時間経過 t-τが加味されて、h(t-τ)となる。別の言い方をすると、単位インパルスを加える時刻をτ遅らせると、出力もτ遅れるので、h(t-τ)で表される。従ってh(t)は、時刻τに関する積分を使って以下の式で表される。これは、事象が一度のみのたたみ込み積分と言うことができる。
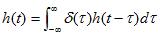
.jpg)
次に、このシステムに単位インパルスではなく、任意の波形 x(t)を入力することを考える。x(t)は、時刻τのx(t)の値x(τ)と単位インパルスのたたみこみ積分とみなすことができ、以下の式で表される。x(τ)倍された単位インパルスを時間をずらしながら加算したものと考えられる。
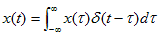
x(t)をインパルス応答h(t)のシステムに入力したときの出力y(t)とすると、上2式より次のたたみ込み積分が成り立つことが導き出される。現在時刻
t における出力波形y(t)は、過去の時刻τにおける入力波形x(τ)と回路の応答 h(t-τ)を使った以下のたたみこみ積分で表される。なお、t<0においてx(t)=0、h(t)=0である因果律を満たすならば、積分期間はτ=0〜∞として構わない。
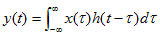
.JPG)
|
| 伝達関数 |
ここで、たたみ込み積分の一般論から話題を転換する。
上記のたたみ込み積分で表される出力関数 y(t) について、ラプラス変換を行ってみると、
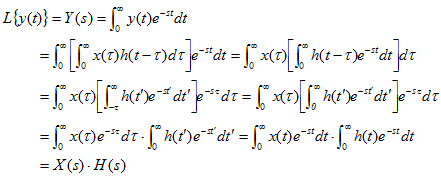 |
----- (11-4)
|
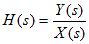 |
----- (11-5) |
と簡単な形で表すことができた。
ここで、X(s)は入力信号のラプラス変換、Y(s)は出力信号のラプラス変換である。
このH(s)を、伝達関数と呼ぶ。これは、(11-4)式の最後の部分から分かるように、対象とするシステム(または回路)のインパルス応答 h(t)のラプラス変換に等しい。
一度そのシステムの伝達関数を求めると、入力信号が変わった場合にも、その伝達関数を計算に使用できるという利点がある。
伝達関数は、特性や安定性を解析するのに使用されるが、対象とするシステムは1入力1出力に限られる。
また、伝達関数を求める場合には、システムのすべての初期値は0でなければならない。この理由は、0でない初期値を認めると、(11-5)式においてY(s)が初期値によって変わることになり、同一システムで伝達関数が違うものになってしまうという矛盾から説明できる。
|
| 極(pole)と零点(zero point) |
伝達関数H(s)が無限大に発散する点を s の値で示し、これを極(pole)という。
伝達関数の分母 = 0 という方程式は特性方程式と呼ばれ、その解を、そのシステムの極、あるいは伝達関数の極という。
極の位置により、過渡応答(自然応答)が決定される。
また、伝達関数が0になる点を s の値で示し、これを零点(zero point)という。
零点とは、それに対応する周波数の駆動で信号応答が伝わらす、出力が0となることを意味する。
|
| 二端子対回路における伝達関数の種類 |
回路解析における伝達関数の入力と出力信号は、定義を明確にすれば回路のどの部分の電圧 ・電流いずれを使っても構わない。
ただし、対象を二端子対回路に限定した場合、明確化のために下表のように呼ぶ場合もある。
s は、複素周波数である。
|
|
|
|
電圧比伝達関数 |
|
|
電流比伝達関数 |
|
|
伝達インピーダンス関数 |
|
|
伝達アドミッタンス関数 |
|
| 伝達関数のまとめ |
・あるシステムを考えるときに、そのシステムをブラックボックスとして、任意の入力に対してどのような出力が得られるかを示しているのが伝達関数である。伝達関数が分かっていれば、入力信号のラプラス変換が得られれば、出力を計算できる。
・別の言い方では、初期状態が0のときの入出力信号のラプラス変換の比を伝達関数と呼ぶ。伝達関数はインパルス応答のラプラス変換であるという言い方もできる。
・伝達関数H(s)は、次の式で表される。この式は、入力信号のラプラス変換をX(s)、出力信号のラプラス変換をY(s)とすると、たたみ込み積分の両辺をラプラス変換することにより得られる。
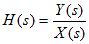
・変数として複素周波数 s=σ+jω を使用することにより、伝達関数が分かればシステムの過渡応答、周波数応答の両方について解析することができる。
・伝達関数をラプラス逆変換せずに s領域のまま解析することでも、多くの情報を得ることができる。
-伝達関数を部分分数展開することで,インパルス応答を発散・減衰・振動などの基本要素に分解できる。
-伝達関数の分母 = 0 とした方程式 (特性方程式) の解の複素平面上での位置が,それらの基本要素の挙動に対応している。
-伝達関数で s=jωと置き換えると周波数応答が得られる。
参考:「やる夫で学ぶディジタル信号処理」 東北大学 大学院情報科学研究科 鏡 慎吾 准教授
|
|
【SPICEによる確認の前に】
市販の主なSPICEには、制御電源にラプラス変換機能が付いています。制御電源にs関数の式を記述し、過渡信号入力を回路に接続することにより、設定したs関数の式を伝達関数として使用できます。このラプラス電源は、複素周波数
s を変数としているので、過渡解析とAC解析で使用できます。出力は、時間関数と周波数関数として得られます。
ただし、ほとんどのSPICEにおいて、過渡解析ではたたみ込み積分を使っているため、コンピュータに大きな負荷となりシミュレーション時間がかかる場合や精度が悪くなる場合があります(例:RLC直列回路の過制動状態の解析)。解決策としては、TopSpice製品版に付属するような、状態空間法モデルを使用する方法があります。
前章で学んだように単位インパルス関数のラプラス変換は、「1」です。したがって上記伝達関数の定義から、ある回路に単位インパルスを入力すると、出力はその回路の伝達関数を逆ラプラス変換したものです。つまり単位インパルスを入力した場合の出力波形は、伝達関数そのものを時間や周波数領域で表したものになります。
下記のファイルの後半でこの確認をしますが、単位インパルスは現実には実現不可能な関数(超関数の一つ)なので、SPICEでできる最大限の近似波形を作っています。またラプラス電源自体も、過負荷となる入力に対しては、理想的には動かないようです。以下の例では、TopSpiceでうまく動いた例を取り上げましたが、他のSPICEでは動かない場合もあります。その逆もありえますが、状態空間法モデルが使えればほとんどの場合、理論通り動作するようです。
|
| SPICEによる確認: RC直列回路の伝達関数 |
| SPICE回路図ファイル |
Transient_Response_RC_Laplace.sch (TopSpice 8 回路図ファイル) |
.jpg) .jpg) クリックで拡大 クリックで拡大 |
| 回路図の作成 |
前章で作成した回路図ファイルでは、(1)SPICEアルゴリズムによる解析と、(2)計算で求めた数式を入力したビヘイビア電源の比較をしました。これに、(3)ラプラス電源を使った解析を追加します。ラプラス電源には、RC直列回路の電圧比伝達関数(1/(CRs+1))と伝達アドミッタンス関数(s/(Rs+1/C))を記述します。これは、sを使って直接インピーダンスを求めたものです。
Demo版には、状態空間法モデルが付属されていないので、回路図でX1とX2の部分は、ディスエーブルとなっています。製品版では、メニューバーにて[Edit]-[Enable
All]とクリックしてこの部分をイネーブル状態にして実行してください。 |
| 解析の設定と実行 |
過渡解析とAC解析の設定をします。2番目の数式を使ったビヘイビア電源は、時間領域の計算なので当然AC解析には、使えません。解析実行後現れるダイアログで、TRANSIENTを選ぶと過渡解析結果が表示され、(1)〜(3)の電圧電流のグラフが得られます。波形表示プログラムのメニューバーより[Plot]-[Auto
plot]とクリックし、AC Sweepを選ぶとAC解析結果が表示され、(1)と(3)の電圧電流の振幅と位相のグラフが得られます。 |
| 解析結果の検討 |
3種類の求め方により得られた電圧電流のグラフは、ほぼ重なり、求めたラプラス変換式が正しいことが分かります。 |
| SPICEによる確認: RL直列回路の伝達関数 |
| SPICE回路図ファイル |
Transient_Response_RL_Laplace.sch (TopSpice 8 回路図ファイル) |
.jpg) .jpg) クリックで拡大 クリックで拡大 |
| 回路図の作成 |
前章で作成した回路図ファイルでは、(1)SPICEアルゴリズムによる解析と、(2)数式入力したビヘイビア電源の比較をしました。これに、(3)ラプラス電源を使った解析を追加します。ラプラス電源には、RL直列回路の電圧比伝達関数(s/(s+R/L))と伝達アドミッタンス関数(1/(Ls+R))を記述します。
Demo版には、状態空間法モデルがついていないので、回路図でX1とX2の部分は、ディスエーブルとなっています。製品版では、メニューバーにて[Edit]-[Enable
All]とクリックしてこの部分をイネーブル状態にして実行してください。 |
| 解析の設定と実行 |
過渡解析とAC解析の設定をします。2番目の数式を使ったビヘイビア電源は、時間領域の計算なので当然AC解析には、使えません。解析実行後現れるダイアログで、TRANSIENTを選ぶと過渡解析結果が表示され、(1)〜(3)の電圧電流のグラフが得られます。波形表示プログラムのメニューバーより[Plot]-[Auto
plot]とクリックし、AC Sweepを選ぶとAC解析結果が表示され、(1)と(3)の電圧電流の振幅と位相のグラフが得られます。 |
| 解析結果の検討 |
3種類の求め方により得られた電圧電流のグラフは、ほぼ重なり、求めたラプラス変換式が正しいことが分かります。 |
| SPICEによる確認: RLC直列回路の伝達関数 |
| SPICE回路図ファイル |
Transient_Response_RLC_Laplace.sch (TopSpice 8 回路図ファイル) |
.jpg) .jpg) クリックで拡大 クリックで拡大 |
| 回路図の作成 |
前章で作成した回路図ファイルでは、(1)SPICEアルゴリズムによる解析と、(2)数式入力したビヘイビア電源の比較をしました。これに、(3)ラプラス電源を使った解析を追加します。ラプラス電源には、RLC直列回路の回路電流/入力電圧のラプラス変換式1/(Ls+R+1/(Cs))を記述します。
回路は、一番上の段が過制動、二番目の段が臨界制動、三番目が減衰振幅となる定数としています。
Demo版には、状態空間法モデルがついていないので、回路図でX1〜X4の部分は、ディスエーブルとなっています。製品版では、メニューバーにて[Edit]-[Enable
All]とクリックしてこの部分をイネーブル状態にして実行してください。 |
| 解析の設定と実行 |
過渡解析とAC解析の設定をします。2番目の数式を使ったビヘイビア電源は、時間領域の計算なので当然AC解析には、使えません。解析実行後現れるダイアログで、TRANSIENTを選ぶと過渡解析結果が表示され、(1)〜(3)の電流のグラフが得られます。波形表示プログラムのメニューバーより[Plot]-[Auto
plot]とクリックし、AC Sweepを選ぶとAC解析結果が表示され、(1)と(3)の電流の振幅と位相のグラフが得られます。 |
| 解析結果の検討 |
3種類の求め方により得られた電圧電流のグラフは、ほぼ重なり、求めたラプラス変換式が正しいことが分かります。 |
| SPICEによる確認: 単位インパルス関数と伝達関数() |
| SPICE回路図ファイル |
Laplace_Transform_exp-at_sin.sch (TopSpice 8 回路図ファイル) |
.jpg) .jpg) クリックで拡大 クリックで拡大 |
| 回路図の作成 |
単位インパルス関数のラプラス変換は、「1」です。したがって伝達関数の定義から、ある回路に単位インパルスを入力すると、出力はその回路の伝達関数を逆ラプラス変換したものです。つまり出力波形は、伝達関数そのものを時間領域で表したものになります。この理論の確認を行います。
まず基準用の減衰振動波形を、ビヘイビア電源で作成します(out1出力)。次にビヘイビア電源に記述した数式を、ラプラス変換し(前章の変換表を使う)、この変換した式を、ラプラス電源に記述します。この電源の入力に単位インパルス関数を入力すると、ラプラス電源の出力(out2)は、入力したビヘイビア電源の出力波形と一致するはずです。
「SPICEによる確認の前に」で述べたように、単位インパルス関数は次のようにして近似波形を作りました。パルス立ち上がり1ns、立下り1ns、パルス幅1ns、パルス振幅値0.5GV。これでパルス面積が1となります。
Demo版には、状態空間法モデルがついていないので、回路図でX1の部分は、ディスエーブルとなっています。製品版では、メニューバーにて[Edit]-[Enable
All]とクリックしてこの部分をイネーブル状態にして実行してください。
|
| 解析の設定と実行 |
過渡解析を実行します。ラプラス電源を使っているため、ステップ上限値を、解析精度と解析時間の兼ね合いで許容できる範囲で小さく設定します。この例では、0〜30msの解析に対して10usとしています。 |
| 解析結果の検討 |
電圧波形は、ほぼ重なり、求めたラプラス変換式が正しいことが分かります。製品版ではout1とout3の誤差は、さらに小さくなります。 |
| SPICEによる確認: たたみ込み積分と伝達関数 (たたみ込み積分の感覚的な理解のために) |
| SPICE回路図ファイル |
Convolution_test_RC1.sch (TopSpice 8 回路図ファイル) |
.jpg) .jpg) クリックで拡大 クリックで拡大 |
| 回路図の作成 |
上述のように線形時不変な回路に、信号を入力したとき結果として現れる出力信号は、たたみ込み積分を使って求められます。RC直列回路を検討対象回路として、単位インパルス波形を入力した場合(1段目)、振幅1のインパルス波形を周期100usと20usで入力した場合(2段目、3段目)、振幅1の方形波を入力した場合(4段目)について、回路図を併記します。各段は、左より通常のSPICE解析回路、ラプラス電源による解析、状態空間法モデル(製品版のみ)による解析となっています。 |
| 解析の設定と実行 |
過渡解析を実行します。ラプラス電源を使っているため、ステップ上限値を、解析精度と解析時間の兼ね合いで許容できる範囲で小さく設定します。この例では、0〜1msの解析に対して1usとしています。 |
| 解析結果の検討 |
結果の波形は、入力、出力と上下に順次並んでいます。
2段目:その出力波形でピーク値等は入力の近似値に依存している。
4段目:周期100us振幅1のインパルス波形入力に対応した結果で、2段目の波形のピーク値を小さくしたものが連続している。
6段目:周期20us振幅1のインパルス波形入力に対応した結果で、全体形状はより方形波入力時の結果(8段目)に近づいている。まだパルス状の入力であるので、その分、出力波形のピーク値は8段目に比べて小さい。そのピーク値は入力パルスのデューティ比に従って大きさが小さくなっている。
8段目:パルスの間隔が0となり、6段目の結果がさらに細かく足し合わされ、平滑化されたものと見ることができる。
|

