|
|
| SPICEで学ぶ電気回路の基礎 講座 |
|
| How to use > 目次 【他のページへは目次のリンクよりジャンプして下さい】 |
|
| 7. 2端子対回路 |
|
| 7.1 2端子対回路とは |
|
入出力とブラックボックス
|
ある機能を持つひとまとまりの電気回路を考える。
回路には、信号や電力を与える入力端子と、外部へつながれる出力端子がある。一般論としては、回路からは多数の入力端子や出力端子を取り出すことができる。
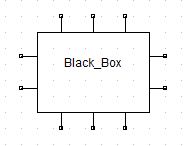
回路の部分をブラックボックス(暗箱)として、個々の内部構成を考えないとすると、N端子の回路は下図(10端子の例)のように表すことができる。
|
| 2端子対回路と2端子対パラメータ |
上記のように一つの電気回路から多数の端子を引き出すことが可能であるが、回路の利用法としての基本は、何らかの入力があり、回路において処理された結果が出力されるという形である。この場合、入出力の信号は電圧電流なので、2つの端子を1組として扱う。
この原則に従い、1組の入力端子対と、もう1組の出力端子対のみを引き出して回路解析することを考える。下図7.1(a)のように回路から入力端子対、出力端子対だけを取り出して解析する場合、この回路を2端子対回路と呼ぶ。
この2端子対回路において、図7.1(b)のように、2端子対回路の入力に電圧v1を加えたとき、入力電流i1とi1'が流れ、そのとき出力電圧がv2で、出力電流i2とi2'が流れたとする。
ここで、以下の3つの条件が成り立つと仮定する。
1) 回路内の使用素子が線形である。(加えたものと結果の電圧電流に比例関係が成り立つ。)
2) 回路内に独立電源を含まない。(発振回路を含まない。線形である従属電源は含んでもよい。)
3) i1=i1'およびi2=i2'が常に成り立つ。
これらの仮定条件により、回路に加えたり結果として現れる電圧電流の変数は、v1,v2,i1,i2の4つとなる。
4つの変数のうち2つがわかれば、残り2つも求まるようにするためには、変数をx、yとしたとき、回路特性が下記のような2元1次連立方程式で表されれば良いはずである。
p=ax+by
q=cx+dy
別の形で書くと
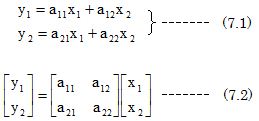
(7.1)式でx1, x2, y1, y2の4変数がv1, v2, i1, i2の4変数にランダムに対応する(x1, x2を独立変数、y1,
y2を従属変数という)。つまり、2端子対回路は4つのパラメータa11〜a22で表すことができる。これを2端子対パラメータという。(7.2)式のように連立方程式を行列で表せば、2端子対パラメータは、2行2列の行列の要素として示される。
任意の2端子対回路の2端子対パラメータがわかれば、任意の入力を与えたときの出力を求めることができるはずである。2端子対パラメータを使うと、回路の内部を考えないですむ、または逆に内部がわからなくてもパラメータを使って解析ができるという利点がある。
(7.2)式でx1, x2の変数に回路変数v1, v2, i1, i2を当てはめる方法は、4種類のものから2つ選ぶ組み合わせとなるので、4C2=6通りある。慣用的にはそのうちの4〜5通りくらいの変数の取り方が使われ、パラメータとしては、Z,Y,F,h,gパラメータなどがある。
2端子対回路に加える電圧・電流は、時間的にどのように変化してもかまわないが、正弦波交流であると仮定した場合には、各パラメータは複素数で表される。Zパラメータの例を以下に示す。
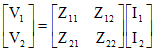
●2端子対パラメータを使うメリット
回路内部の動作は知る必要がなく、回路をブラックボックスとみなして、入力に対する出力の関係だけがわかればよい場合に
1) 一度、2端子対パラメータを求めておくと、入出力条件が変わっても、新しい条件を当てはめて、パラメータはそのままで計算し直すことができる。
2) Fパラメータがわかっている2つの回路の縦続接続、Yパラメータがわかっている2つの回路の並列接続、Zパラメータがわかっている2つの回路の直列接続について、簡単に求めることができる。
●信号が交流の場合
2端子対回路に加える電圧・電流は、時間的にどのように変化してもかまわないが、ここでの議論はマイクロウェーブ以上などの高周波の場合は除くものとする。その場合には、集中定数回路として電圧・電流で解析することは、現実にそぐわなくなる。代わりに電力・エネルギーを変数としなければならなくなり、Sパラメータの概念が必要になる。
|
|
|
|
| 7.2 代表的な2端子対パラメータ |
|
| 2端子対パラメータの求め方 |
下記回路のZパラメータを例にして、二通りの2端子対パラメータの求め方を述べる。
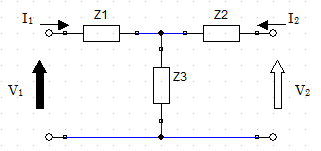
1) 回路方程式を立てる。――内部回路構成がわかっていて、比較的簡単な2端子対回路の場合
入力に電圧源V1、出力に電圧源V2を接続したとき、閉路解析法により
V1=(Z1+Z3)I1+Z3I2
V2=(Z2+Z3)I2+Z3I1=Z3I1+(Z2+Z3)I2
が立てられるので、係数を比較して
Z11=Z1+Z3, Z12=Z3, Z21=Z3, Z22=Z2+Z3
2) パラメータの定義により計算または実測する。
――内部回路構成がわからないか、わかっていても方程式が立てにくい場合
I2=0のとき、V1/I1=Z11=Z1+Z3
I1=0のとき、V1=I2Z3なので、Z12=V1/I2=Z3
I2=0のとき、V2=I1Z3なので、Z21=V2/I1=Z3
I1=0のとき、V2/I2=Z22=Z2+Z3
このとき次項で述べる相反定理が成り立つならば、Z12=Z21であるので、Z12またはZ21の残った片方の計算は省略できる。 |
相反定理
または
可逆定理 |
2端子対回路で、ある端子対側(ポート1)に電圧源Vをつないだときに、逆の端子対側(ポート2)を短絡したときにそこを流れる電流が I だったとする。同じ回路を使ってポート2側に電圧源Vをつないで、ポート1を流れる短絡電流を測ると
I に等しい。この場合に、2端子対回路に求められる条件は、独立電源も従属電源も含まない線形な受動素子のみで構成される回路であること。
また今度は、ポート1に電流源 I をつないだときに、ポート2に現れた電圧がVだったとする。この回路のポート2側に電流源 I をつなぎ、ポート1に現れる電圧を測るとVに等しい。
この定理を知っていると、この定理が成り立つ回路では7.4項の表の相反条件が成立するということなので、2端子対パラメータ計算を簡単にすることができる。
[ Zパラメータでの証明 ]
V1=Z11I1+Z12I2 ------ (7.3)
V2=Z21I1+Z22I2 ------ (7.4)
が成り立つとき、ポート2を短絡してV2=0とすると、(7.4)式より
0=Z21I1+Z22I2
I1を求め I1=-Z22/Z21・I2 これを(7.3)式に代入して
V1=Z11I1+Z12I2=-Z11Z22/Z21・I2+Z12I2
=(Z12Z21-Z11Z22)/Z21・I2
したがってV2=0としたときの出力端短絡伝達インピーダンス
V1/I2=(Z12Z21-Z11Z22)/Z21 ------ (7.5)
また、ポート1を短絡してV1=0とすると、(7.3)式より
0=Z11I1+Z12I2
I2を求め I2=-Z11/Z12・I1 これを(7.4)式に代入して
V2=Z21I1+Z22I2=Z21I1+-Z11Z22/Z12・I1
=(Z21Z21-Z11Z22)/Z12・I1
したがってV1=0としたときの入力端短絡伝達インピーダンス
V2/I1=(Z12Z21-Z11Z22)/Z12 ------ (7.6)
ここで、(7.3)(7.4)式をブラックボックス回路の閉路電流の式とみると
インピーダンス行列の対角成分Z11とZ22は、それぞれ1番目と2番目の閉路電流が流れているインピーダンスの
総和を表し、非対角成分Z12とZ21は、どちらも1番目と2番目の閉路の共通のインピーダンス代数和を表している。
したがって、Z12=Z21である。インピーダンス行列は対称行列である。
上記の結果Z12=Z21を、(7.5)と(7.6)式に当てはめると、
V2=0のときのV1/I2 と V1=0のときのV2/I1は、等しい。(証明終)
|
| SPICEによる確認: Yパラメータ計算の確認 |
| SPICE回路図ファイル |
Y-parameters_2-port_4.zip (TopSpice 8 回路図ファイル + **.MISファイル) |
|
|
| 回路図の作成 |
上図のような回路を作成し、Yパラメータを定義に従い計算します。Y11=jωC1+1/(jωL) Y12=-1/jωL=Y21 Y22=1/jωL+jωC2/(1+jωRC2)
これらパラメータに数値を入れたものをアナログ ・ビヘイビア ・モデルでつくったサブサーキットY_para_2Port(オリジナル)に入力します。このサブサーキットは、ラプラス変換モデルを使用しています。
|
解析の設定と実行
(AC解析と過渡解析) |
AC解析(周波数範囲1Hz〜1MHz)と、過渡解析(適当なパルス波形を入力)を行います。 |
| 解析結果の検討 |
素子をつないで作成した回路の特性と、計算で求めたYパラメータによるビヘイビア ・モデルの特性が、AC解析、過渡解析ともに同一となりました。Yパラメータの計算が合っていたことが確認できました。 |
| SPICEによる確認: 相反定理の確認 |
| SPICE回路図ファイル |
Reciprocity_1.sch (TopSpice 8 回路図ファイル) |
|
|
| 回路図の作成 |
上図のような任意の回路を作成します。ただし相反定理が成り立つための条件として、回路は受動素子のみで構成し、独立電源や従属電源は含まないものとします。回路は、上段の2つが、電圧源を入力し出力電流を測る場合で、入出力を交換しています。下段の2つは、電流を入力し、出力電圧を測定しています。上段同様に入出力を交換しています。
上段のE1や下段のG1、G2は従属電源で、単に、信号源を4つ用意し各種解析の設定をする手間を省くために使用しています。E1は電圧制御電圧源でV1で設定した内容を1倍して入力します。G1,G2は電圧制御電流源で、この場合はV1電圧を1/1000倍して回路に入力します。 |
解析の設定と実行
|
一度の解析実行でAC解析、DC解析、過渡解析を行っています。 |
| 解析結果の検討 |
電圧入力、電流入力どちらの場合も、各種解析において相反定理が成り立つことが確認できました。適当な箇所に従属電源を挿入してみると、相反定理が成り立たなくなることもわかります。
なお、各解析結果は一度の解析実行後、波形表示プログラムのメニューでPlot->Auto plotと選ぶことで再実行しないで別の解析結果に移動してください。 |
|
|
|
| 7.3 複数回路の接続 |
|
Fパラメータによる縦続接続
|
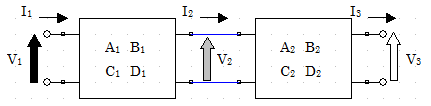
上図のように二つの2端子対回路が縦一列に接続されている場合を考える。増幅回路などの例のように、一般的にはもっとも多い接続方式と思われる。この接続方法を縦続接続(Cascade Connection)という。
各2端子対回路のFパラメータが、それぞれ図の値であるとわかっているとすると、縦続行列の定義よりそれぞれ以下の式が成立する。
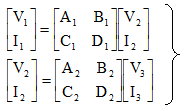 |
-------- (7.7) |
(7.7)の下式の行列を上式に代入して、
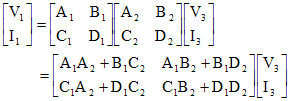 |
|
| --------- (7.8) |
したがって、縦続接続された回路の全体のFパラメータは、(7.8)式のように各縦続行列の積で求められる。
|
Yパラメータによる並列接続
|
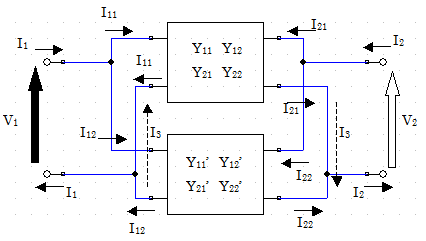
上図のように二つの2端子対回路の入力対と出力対同士が接続されている場合を考える。この接続方法を並列接続(Parallel Connection)という。
各2端子対回路のYパラメータが、それぞれ図の値であるとわかっているとすると、アドミッタンス行列の定義より図中の回路変数を使ってそれぞれ以下の式が成立する。
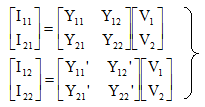 |
---------- (7.9) |
ここで、並列接続回路全体を一つの2端子対回路とみたときの電流I1とI2は、上図で決めたように
I1=I11+I12 および I2=I21+I22 であるので、行列で表し、(7.9)式を当てはめると、
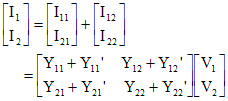 |
|
| ---------- (7.10) |
したがって、並列接続された回路の全体のYパラメータは、(7.10)式のように各Yパラメータ成分同士の和で表される。ただし、並列接続することによってI3のような独立な環路電流が流れる場合は、単独の2端子対回路の条件が満たされないことになるので(7.10)式の関係は成立しない。 |
Zパラメータによる直列接続
|
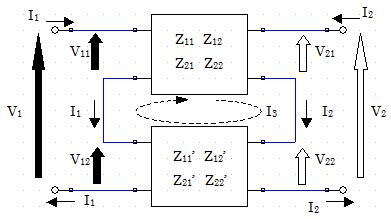
上図のように二つの2端子対回路の片方の入力同士と片方の出力同士が接続されている場合を考える。この接続方法を直列接続(Series Connection)という。2端子対回路では、この形が直列接続であり、縦続接続との呼び名や接続方法の混同に気をつける。
各2端子対回路のZパラメータが、それぞれ図の値であるとわかっているとすると、インピーダンス行列の定義より図中の回路変数を使ってそれぞれ以下の式が成立する。
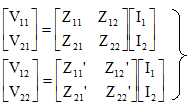 |
---------- (7.11) |
ここで、直列接続回路全体を一つの2端子対回路とみたときの電流V1とV2は、上図で決めたように
V1=V11+V12 および V2=V21+V22 であるので、行列で表し、(7.11)式を当てはめると、
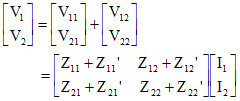 |
|
| ---------- (7.12) |
したがって、直列接続された回路の全体のZパラメータは、(7.12)式のように各Zパラメータ成分同士の和で表される。ただし、直列接続することによってI3のような独立な環路電流が流れる場合は、単独の2端子対回路の条件が満たされないことになるので(7.12)式の関係は成立しない。
|
|
|
|
|
| 7.4 2端子対パラメータの相互変換 |
|
|
パラメータ
|
Z
|
Y
|
h
|
F
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Δ(行列式)
|
|
|
|
|
|
相反条件
|
|
|
|
|
回路形態により、求めやすい計算しやすいパラメータとそうでないものがある。複数回路に分けられる場合も、縦列接続、並列接続、直列接続はそれぞれパラメータが限定される。計算しにくいパラメータを求めたい場合、計算しやすいパラメータを求め、この表により変換するとよい。
*FパラメータにおけるI2の向きのみ、他と逆になるので注意する。
|
|
|
| SPICEによる確認: 複数回路の接続とパラメータの相互変換 |
| SPICE回路図ファイル |
Y-parameters_2-port_Twin-T.zip (TopSpice 8 回路図ファイル + **.MISファイル) |
|
|
| 回路図の作成 |
図のようなツインT型回路を作成します。確認は既出のYパラメータのアナログ ・ビヘイビア ・モデルを使用します。
パラメータの求め方としては、計算しやすいので各T型回路のZパラメータを求め、それぞれYパラメータに変換します。2つのT型回路の並列接続となっているので、各Yパラメータ成分を加算し、合計のパラメータを求めます。
|
解析の設定と実行
|
一度の解析実行でAC解析、DC解析、過渡解析を行っています。 |
| 解析結果の検討 |
素子をつないで作成した回路の特性と、計算で求めたYパラメータによるビヘイビア ・モデルの特性が、AC解析、DC解析、過渡解析ともに同一となりました。Zパラメータ、Yパラメータの計算が合っていたことが確認できました。 |
|
|
|
|
|
|

