ひずみ波の実効値
|
正弦波の場合と同様に、ひずみ波を回路に入力したときの消費電力を知りたい場合がある。ひずみ波は、基本波に高調波が加わったもので表されることがわかったので、基本波のみの場合より消費電力は大きくなると予想される。
まず、電圧電流の実効値を求める。
ひずみ波 f(t) が、式(8.3)のようにフーリエ級数展開されたとする。計算しやすくするため、以下のように式(8.3)の直流分を別に書く。
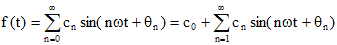
実効値は、その定義から二乗平均平方根とも呼ばれる、時間的に変動している信号の平均を示すひとつの方法である。まず、f(t) の二乗を求める。
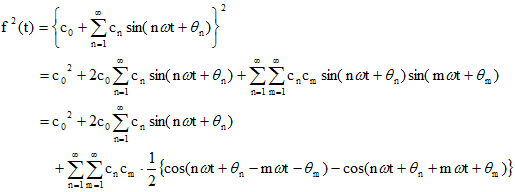
ここで、第3項の式の変形は以下の三角関数の公式を使っている。
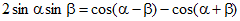
この結果を、1周期にわたって平均する(二乗平均)。上式の第2項は正弦波の平均なので0となる。第3項は、n≠mにおいては余弦波の平均となりすべて0となる。n=mにおいてのみ、cos(0)=1となり0以外の値をとる。
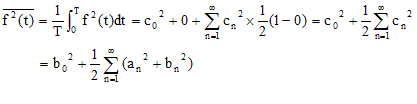
したがって、実効値は以下のように表される。
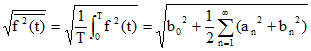 |
------ (8.8) |
式(8.3)に示すように、b0は直流成分であり、anとbnは第n高調波の振幅である。つまり
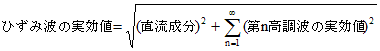
|
ひずみ波の電力
|
次にひずみ波の消費電力を求める。ひずみ波の電圧と電流が以下の式で表されるとする。θnは各周波数ごとの電圧電流間の位相差を示す。
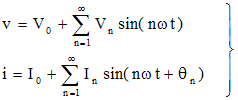
瞬時電力 p (W) は以下のように計算される。
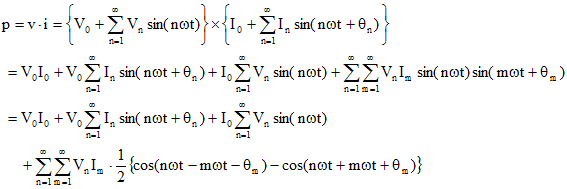
第4項の式の変形は、前項で述べた三角関数の公式を使っている。
瞬時電力の時間平均である平均電力P(W)を求める。
上式の第2項と第3項は正弦波の平均なので0となる。第4項は、n≠mにおいては余弦波の平均となりすべて0となる。n=mにおいてのみ、cos(0-θm)となり0以外の値をとる。
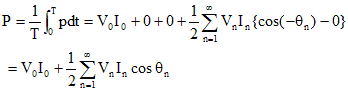 |
------ (8.9)
|
これより、ひずみ波の電力は以下のように正弦波交流の電力を高調波まで拡張したものと言える。

|
ひずみ率
|
周期性をもつひずみ波が、正弦波からどの程度ひずんでいるかを示すひとつの基準にひずみ率がある。
ひずみ率は、ひずみ成分が多いほど100%に近づいていく。正弦波はひずみ率0%である。
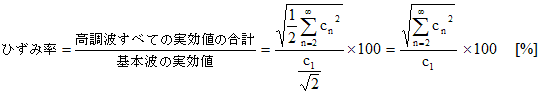
ここで、以下のような矩形波のひずみ率を求めてみる。
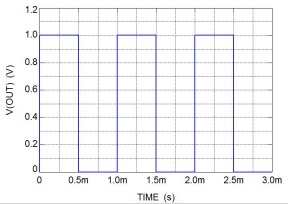
この波形をフーリエ級数展開した式は
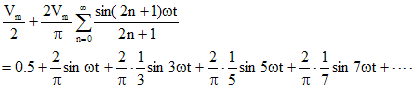
したがって、ひずみ率は以下のように45.0%と求められる。
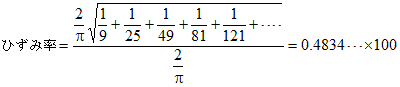
|
| SPICEによる確認: ひずみ波の実効値と平均電力 |
| SPICE回路図ファイル |
Fourier_Power_0.sch (TopSpice 8 回路図ファイル) |
.jpg) .jpg) クリックで拡大 クリックで拡大 |
| 回路図の作成 |
LCR直列回路にひずみ波電圧を入力したときの、実効値電圧、実効値電流、回路で消費される平均電力をそれぞれ求めてみます。ひずみ波はv=1+sinωt+cos2ωt、基本周波数f=1kHzとします。計算簡略化のために、R=1Ω,1/ωC=2,ωL=1とします。ひずみ波の入力信号電圧は、これまで同様、信号源2つを足し算して作ります。 |
| 解析の設定と実行 |
過渡解析を行いますが、瞬時値ではなく実効値、平均電力をSPICEの関数、それぞれRMS,AVGを使って計算させるので、十分時間が経過して定常状態となったグラフが必要です。過渡解析は、0〜50msまで行い、表示は30m〜50msとします。正確な値に近づけるには、ある程度の分解能が必要です。最大時間ステップを50msの1/50000の1usとしました。 |
| 解析結果の検討 |
瞬時値電圧は、v=1+sinωt+cos2ωtなので、(8.8)式により、実効値電圧は
Ve=√(1^2+1/2(1^2+1^2))=√2=1.414213... → SPICEでは1.4142
また、瞬時値電流は、基本波と第2高調波別々の計算結果を合成して、
i=1/√2・sin(ωt+45°)+1/√2・sin(2ωt-45°)となる。したがって、(8.8)式より実効値電流は、
Ie=√(1/2(1/2+1/2))=1/√2=0.707106... → SPICEでは0.7071
平均電力は、(8.9)式より
P=1/2(1/√2・cos45°+1/√2・cos(-45°))=1/2×(1/2+1/2)=0.5 → SPICEでは0.500
SPICEでは、t=50msの値をカーソルを使って読み取ります。
|
| SPICEによる確認: フーリエ級数展開とひずみ率 |
| SPICE回路図ファイル |
Distortion_Rate_1.sch (TopSpice 8 回路図ファイル) |
.jpg) .jpg) クリックで拡大 クリックで拡大 |
| 回路図の作成 |
上記で計算した矩形波を電圧信号源で発生させます。 |
| 解析の設定と実行 |
過渡解析を行います。そのとき同時にフーリエ解析の設定を行います。これは、元祖バークレーSPICEについていた機能で、過渡解析結果の指定された信号をフーリエ級数展開し、表にして出力ファイルに表示するというものです。一部の市販SPICEでは、次項のFFTがあれば不要ということで機能がついていないものもあるようですが、PSpice,LTspice,TopSpiceではこの機能が残されています。基本周波数と第何次高調波まで計算させるか、出力変数を指定します。ここでは基本周波数1kHz、第15高調波まで、出力V(out)としたいので、コマンドとしては、以下のようになります。
.FOUR 1000 15 V(out)
過渡解析の設定で注意すべきは、級数展開計算精度に直接影響するので、
(1)(最大)時間ステップを小さく設定すること(PSpiceなどでは出力ファイルへの印刷時間間隔)、また、
(2)解析終了時間をなるべく大きくとること、です。
級数展開の計算は、過渡解析終了時間の手前1周期分についてのみ行われますが、そのときの目標波形は、十分時間が経過した状態で過渡的な変化がなくなった定常状態である必要があるからです。
|
| 解析結果の検討 |
素上記の数式から導いた理論値は、
直流分 0.5V,基本波 0.6366V,第3高調波 0.2122V,第5高調波 0.1273V,第7高調波 0.09094V・・・
ひずみ率は、48.34・・% (n=7では44.99900%) となっています。
出力ファイルに表形式で示されているSPICEの計算結果は、
直流分 0.500V,基本波 0.6366V,第3高調波 0.2122V,第5高調波 0.1273V,第7高調波 0.09095V・・・
ひずみ率は、44.999%(n=7であるため)です。
出力ファイルを見るには、波形表示プログラムのメニューから、Tools->Browse Output Fileとクリックします。
|
| SPICEによる確認: 高速フーリエ変換(Fast Fourier Translation:FFT) |
| SPICE回路図ファイル |
Distortion_Rate_2.sch (TopSpice 8 回路図ファイル) |
.jpg) .jpg) クリックで拡大 クリックで拡大 |
| 回路図の作成 |
前項で使った同じ回路を使用します。 |
| 解析の設定と実行 |
FFTを行う場合は、基本的には事前にフーリエ解析の設定は必要ありません。過渡解析の設定のみ行い、結果の波形に対してFFTを行うという手順になります。SPICEのFFT解析自体で、設定項目はありません。FFT機能は、元祖バークレーSPICEにはなく、一般的に商用SPICEの波形表示プログラムに付けられた機能です。
TopSpiceでは、波形表示プログラムにおいて、Toransform->FFTと選んでください(上記回路図ファイルでは設定済み)。あとは表示された結果のグラフの希望する部分を拡大するだけです。
ただしFFTを行う場合、過渡解析の設定において、以下の注意点があります。
まず、フーリエ級数展開と同じ理由で、計算精度を上げるため、
(1)時間ステップまたは最大時間ステップを小さく設定すること。
また、フーリエ変換のアルゴリズム上の理由で
(2)過渡解析終了時間を、基本波周期の正確な整数倍とすること、
さらに、これも級数展開と同じ理由で、目標波形は、十分時間が経過した状態で過渡的な変化がなくなった定常状態である必要があるので、
(3)解析終了時間をなるべく大きくとること、です。 |
| 解析結果の検討 |
上記の結果のグラフからカーソルを使って、各周波数の振幅値を読み取ると、
直流分 0.500V,基本波 0.6366V,第3高調波 0.2122V,第5高調波 0.1273V,第7高調波 0.09094V・・・
波形の一部拡大の方法は、「+」キーを押すとカーソル形状が変わるので、目標部分の対角線をドラッグします。
|

